Euclidean Distance
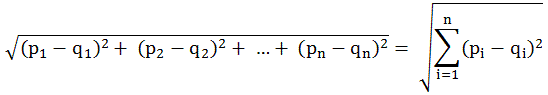
위 공식은 유클리드라는 사람이 만든 N차원에서의 두 점간의 거리를 구하는 공식이다.
재미있는 문제를 풀어보다 이 공식으로 문제를 풀어야 해서 찾아보았고 역시나.
기초 수학이 부족해 루트부터 다시 개념잡고 공부!
일단 p와 q는 점을 나타낸다.
p1, q1은 각 점들의 좌표다. 예를 들어 2차원공간에서의 좌표를 나타낼때
우리는 보통 x, y로 좌표를 표현하는데 이 것을 위의 공식으로 나타내면
첫번째 점의 x, y좌표는 p1, p2로 나타낼수 있고, 두번째 점의 x, y좌표는 q1, q2로 나타낼 수 있다.
3차원이라면 x, y, z, p1, p2, p3이다.
2차원을 예로 들어 보자.
첫번째 점 p의 좌표는 (x=3, y=4)이고 두번째 점 q의 좌표가(x=2, y=11)이라고 할때 위의 공식으로 식을 만들어 풀어보면 아래와 같다.
1. 루트 ( (3 - 2)^2 + (4 - 11)^2 )
2. 루트 ( 1 + -7^2)
3. 루트 ( 1 + 49 )
4. 7.0710...
이 공식은 2차원 공간에서 1사분면뿐 아니라 4사분면으로 나누어진 2차원공간에서도 유효하다.
내 친구이자 나의 프로그래밍 스승인 쏭겐님께서 피타고라스의 정리를 이용해서 설명을 해주는데.
참 그넘 잘한다.ㅎㅎ
어쨌든 친구 덕분에 더욱 확고히 이해할 수 있었고 까먹기도 쉽지 않을정도가 되었다. (땡큐)
이대로 그냥 끝내면 재미없으니까 자바스크립트로 예제 코드를 한번 짜 보았다.
------------------------------------------------------------------------------------------------
먼저 위와 같은 2차원상에서의 좌표를 나타내는 객체를 하나 정의하고 이를 이용해 2차원상에서의
두 점간의 거리를 구하는 유클리디안 함수를 만들어 보면 아래와 같다.
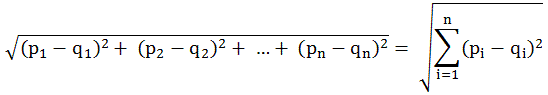
위 공식은 유클리드라는 사람이 만든 N차원에서의 두 점간의 거리를 구하는 공식이다.
재미있는 문제를 풀어보다 이 공식으로 문제를 풀어야 해서 찾아보았고 역시나.
기초 수학이 부족해 루트부터 다시 개념잡고 공부!
일단 p와 q는 점을 나타낸다.
p1, q1은 각 점들의 좌표다. 예를 들어 2차원공간에서의 좌표를 나타낼때
우리는 보통 x, y로 좌표를 표현하는데 이 것을 위의 공식으로 나타내면
첫번째 점의 x, y좌표는 p1, p2로 나타낼수 있고, 두번째 점의 x, y좌표는 q1, q2로 나타낼 수 있다.
3차원이라면 x, y, z, p1, p2, p3이다.
2차원을 예로 들어 보자.
첫번째 점 p의 좌표는 (x=3, y=4)이고 두번째 점 q의 좌표가(x=2, y=11)이라고 할때 위의 공식으로 식을 만들어 풀어보면 아래와 같다.
1. 루트 ( (3 - 2)^2 + (4 - 11)^2 )
2. 루트 ( 1 + -7^2)
3. 루트 ( 1 + 49 )
4. 7.0710...
이 공식은 2차원 공간에서 1사분면뿐 아니라 4사분면으로 나누어진 2차원공간에서도 유효하다.
내 친구이자 나의 프로그래밍 스승인 쏭겐님께서 피타고라스의 정리를 이용해서 설명을 해주는데.
참 그넘 잘한다.ㅎㅎ
어쨌든 친구 덕분에 더욱 확고히 이해할 수 있었고 까먹기도 쉽지 않을정도가 되었다. (땡큐)
이대로 그냥 끝내면 재미없으니까 자바스크립트로 예제 코드를 한번 짜 보았다.
------------------------------------------------------------------------------------------------
function Point(x, y) {
this.x = x || 0;
this.y = y || 0;
}
Point.prototype.equals = function(point) {
if (!point || point.constructor != Point) {
return false;
}
return this.x === point.x && this.y === point.y;
}
Point.prototype.xPoint = function(x) {
if (typeof x == "undefined") {
return this.x;
} else {
this.x = x;
}
}
Point.prototype.yPoint = function(y) {
if (typeof y == "undefined") {
return this.y;
} else {
this.y = y;
}
}
먼저 위와 같은 2차원상에서의 좌표를 나타내는 객체를 하나 정의하고 이를 이용해 2차원상에서의
두 점간의 거리를 구하는 유클리디안 함수를 만들어 보면 아래와 같다.
function EuclideanDistance(point1, point2) {
return point1.equals(point2) ? 0 :
Math.sqrt(
Math.abs(
Math.pow(point1.xPoint() - point2.xPoint(), 2) +
Math.pow(point1.yPoint() - point2.yPoint(), 2))
);
}
'language > javascript' 카테고리의 다른 글
| 자바스크립트로 시스템 클립보드 접근하기 (Access to the system clipboard in JavaScript.) (0) | 2015.09.22 |
|---|---|
| Google Closure Tools (0) | 2010.02.18 |
| 웹에디터 FCKeditor (J2EE 환경에서 사용) (2) | 2009.03.25 |